AFFINES (ESPACE ET REPÈRE)

AFFINES (ESPACE ET REPÈRE)

AFFINES ESPACE & REPÈRE

Dans la conception intuitive de l’espace usuel, il n’y a pas d’origine privilégiée; c’est une fois qu’une origine est choisie que cet espace devient un espace vectoriel. La structure d’espace affine formalise cette situation à partir de la notion de translation associée à un vecteur d’extrémités données, défini comme bipoint. Plus précisément, la structure affine se définit comme suit.

Espace affine . Soit E un espace vectoriel sur un corps commutatif K. Un ensemble A est dit espace attaché à l’espace E s’il est muni d’une application de A 憐 E dans A, notée (M, x ) 料 M + x , telle que le groupe additif de E opère simplement transitivement sur A. Autrement dit, à (M, x ) 捻 A 憐 E correspond un point N de A et un seul, tel que N = M + x ; et à un couple quelconque de points (M, N) de A 憐 A, que l’on désigne sous le nom de bipoints, correspond dans E un vecteur x (appelé opérateur de translation de A) et un seul, tel que N = M + x . Ce vecteur x se note MN . Deux bipoints AB et CD sont dits équipollents si AB = CD.

Soit O un point quelconque de A. Le couple (A, O) s’appelle espace affine muni de l’origine O. L’application de A dans E, définie par M 料 x = OM, est une bijection qui permet d’identifier l’espace A muni de l’origine O à l’espace vectoriel E.

Réciproquement, par l’application qui à tout couple de vecteurs (x , y ) de E associe le vecteur x + y , l’ensemble E devient un espace affine attaché à l’espace vectoriel E. Le vecteur nul de E s’appelle origine canonique de l’espace affine E.

Si l’espace E est de dimension finie, on pose dim (A) = dim (E).

Variété linéaire affine . Un sous-ensemble A 說 A est appelé variété linéaire affine (ou variété linéaire) de l’espace affine A si, pour toute famille finie de points de A , tout barycentre de ces points appartient à A . Une condition nécessaire et suffisante pour qu’une partie non vide A de A soit une variété linéaire affine est que, en prenant un point O quelconque dans A , l’ensemble des vecteurs OM, où M 捻 A , soit un sous-espace vectoriel E de l’espace vectoriel E auquel est attaché A. Le sous-espace E ne dépend d’ailleurs pas du choix de O dans A . D’autre part, on peut montrer que la variété linéaire A est un espace affine attaché à E (qui est appelé direction de A ). Si E est de dimension finie, on pose: dim (A ) = dim (E ). Étant donné un sous-ensemble B de A, on appelle variété linéaire affine engendrée par B la plus petite variété linéaire contenant B; on montre que c’est l’intersection de toutes les variétés contenant B. D’autre part, la variété linéaire affine engendrée par (k + 1) points de A notés (aⁱ ), pour 1 諒 i 諒 k + 1, est l’ensemble des barycentres des aⁱ , Par définition, les (k + 1) points aⁱ sont dits affinement indépendant (ou forment une famille affinement libre) si la dimension de la variété linéaire qu’ils engendrent est égale à k ; si cette dimension est inférieure à k , ils sont dits affinement lié.

Repère affine . On appelle repère affine d’un espace affine A attaché à un espace vectoriel E de dimension n la donnée d’un point O de A et d’une base 龍 de E. Le point O est l’origine du repère et les coordonnées d’un point M sont les composantes de OM sur la base 龍. Ainsi, si:

pour 1 諒 i 諒 n , et si:

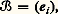
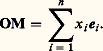les coordonnées de M sont les xⁱ .

Géométrie affine. La géométrie affine est l’étude des espaces affines et des variétés linéaires affines ainsi que des invariants par le groupe affine.

Encyclopédie Universelle. 2012.